K-Means的運作原理

1. 人工決定樣本需分為K類
2. 隨機給定K個中心點(未必為有資料所在的點，可能為任意一點)
3. 計算每個資料點離K個中心點之間各自的距離，根據距離指派該樣本點至最接近的中心點，使其和中心點所屬的分類相同
4. 找出各類所屬的資料點，計算各類新的中心點，並將舊中心點替換掉
5. 重複3和4的步驟，直到中心點不再更動

優點：
計算速度快
模型運算方式較容易理解
缺點：
使用平均值的算法容易受到離群值的影響
對於類別性變數並不適用平均數，因此僅適用於數值型變數
各類樣本數差異較大時，容易產生錯誤分類

K-Medoids

K-Medoids和K-Means的方式類似，步驟如下：

1. 人工決定樣本需分為K類
2. 隨機給定K個中心點(使用資料點作為中心)
3. 計算每個資料點離K個中心點之間各自的距離，根據距離指派該樣本點至最接近的中心點，使其和中心點所屬的分類相同
4. 找出各類所屬的資料點，計算類別中樣本點之間的距離，將距離所有資料點最近的資料點當作新的中心，並將舊中心點替換掉
5. 重複3和4的步驟，直到中心點不再更動

K-Medoids和K-Means的差異僅有兩處，分別為中心點的選擇(K-means:虛擬點v.s K-medoids實際樣本點)和中心點決定的方式(K-Means:群內樣本的座標平均值v.s K-medoids: 群內距離和最小的樣本點)。由於決定中心點的方式不同，因此K-Medoids較不容易受到離群值的影響，且可以處理類別型資料，但運算量相對而言較大。

Kmeans實作

R:使用內建的stats套件中的kmeans

set.seed(123)
# 建立模型，一開始假設nstart群
kmeans_model <- kmeans(testing[,1:12], centers = 13, nstart = 25,iter.max = 300)
# 找出分群結果
pred_kmeans <- as.factor(kmeans_model$cluster-1) ## activity 起始值為0
# 衡量
confusionMatrix(pred_kmeans,reference =  as.factor(testing$Activity))

根據混淆矩陣可知，kmeans的結果並不好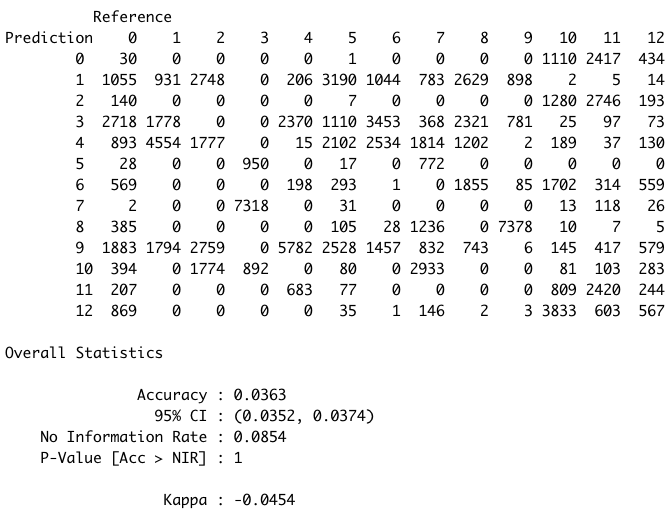

## 視覺化結果，使用其中一個加速度計的xy軸數值，作為視覺化呈現
library(cluster)
y_kmeans <- kmeans_model$cluster-1
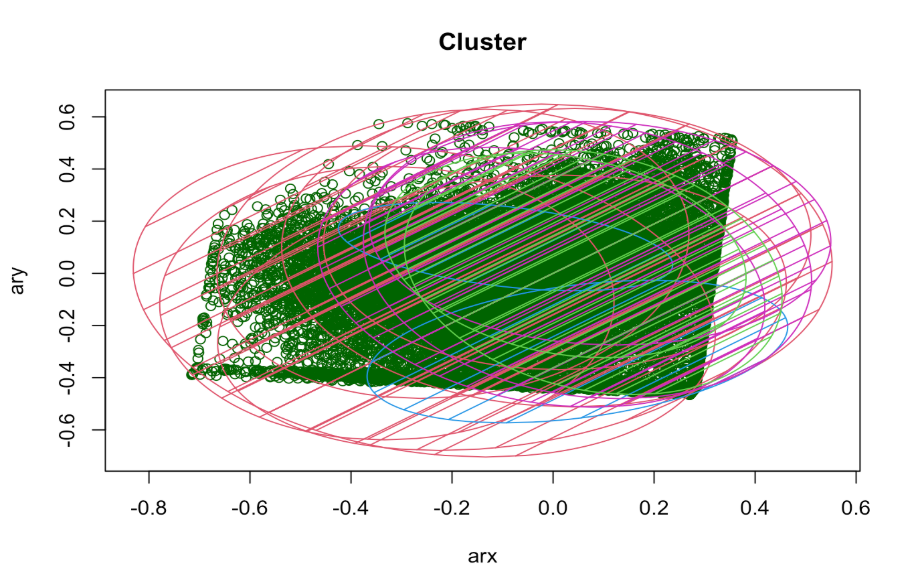
clusplot(testing[, c("arx", "ary")],y_kmeans,lines = 0,
         shade = TRUE,color = TRUE,
         labels = 2,plotchar = FALSE,
         span = TRUE,
         main = paste("Cluster"),
         xlab = 'arx',
         ylab = 'ary')

Python: sklearn.cluster套件中的KMeans

from sklearn import cluster

# 建立模型
pred_kmean = cluster.KMeans(n_clusters = 13,algorithm="elkan")
# 預測分群結果
pred_kmean.fit_predict(X_test)
pred_labels = pred_kmean.labels_
# 衡量結果
from sklearn import metrics
print(metrics.classification_report(pred_labels, Y_test))

根據混淆矩陣可知，kmeans的分群結果並不好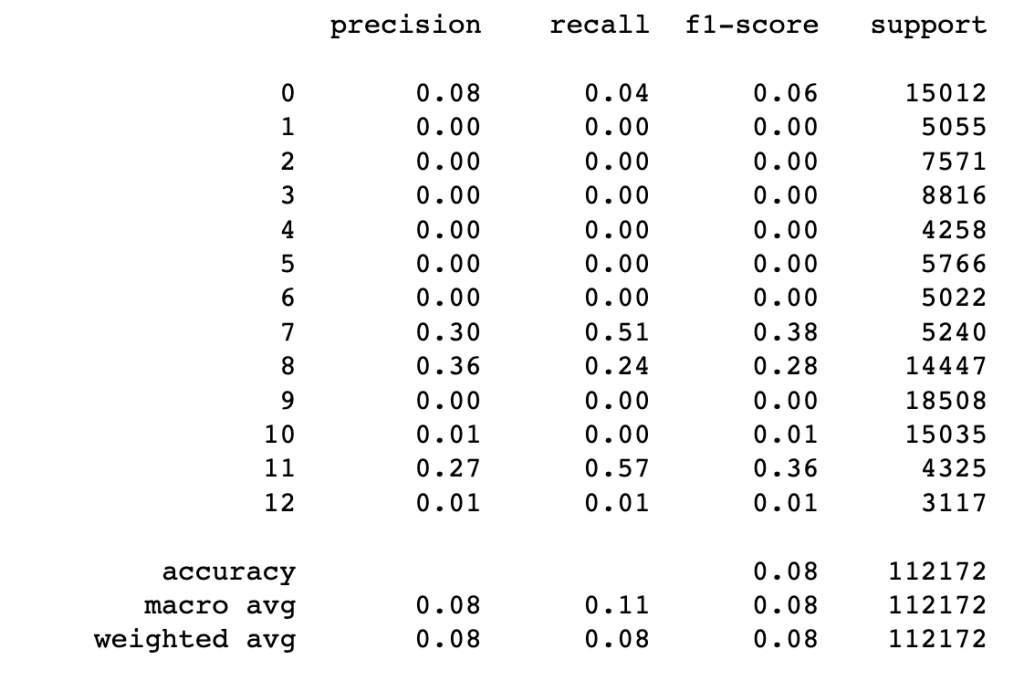

K-Medoids實作

R:使用內建的cluster套件中的pam

library(cluster)

# 為了減小計算量，因此隨機在testing set中抽取了10000筆資料來做示範
subset_testing <- testing[sample(1:length(testing$Activity),10000),]
# 模型
model_kmedoids <- pam(subset_testing[,1:12], 13)
# 預測分群結果
pred_kmedoids <- as.factor(model_kmedoids$clustering-1)
# 衡量結果
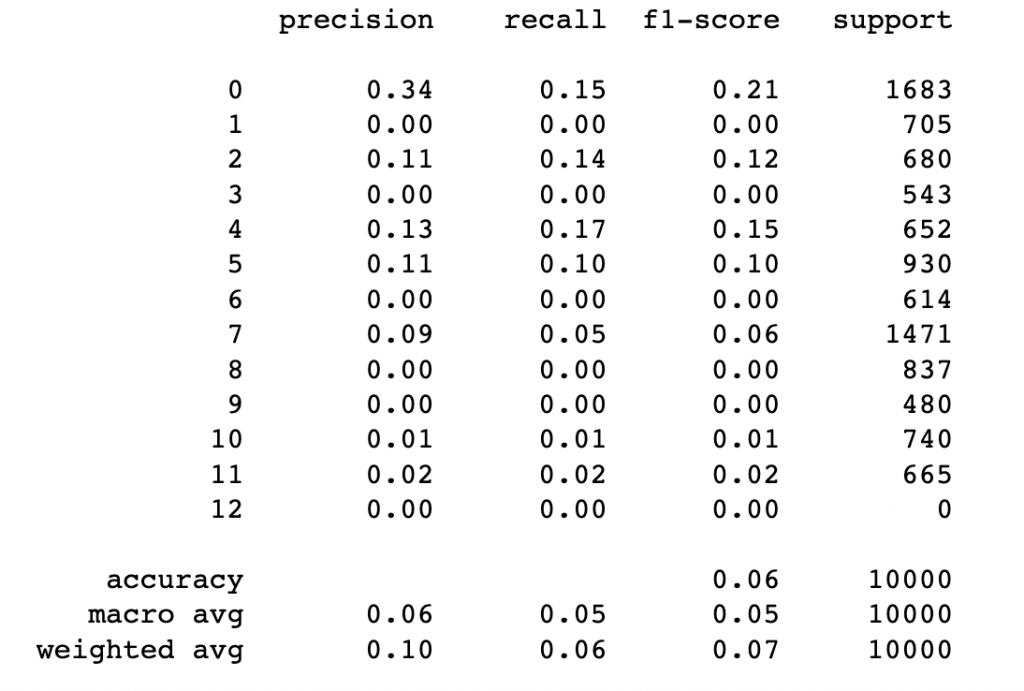
confusionMatrix(pred_kmedoids,reference =  as.factor(subset_testing$Activity))

Python: sklearn_extra.cluster套件中的KMedoids

from sklearn_extra.cluster import KMedoids

# 為了減小計算量，因此隨機在testing set中抽取了10000筆資料來做示範
index = list(range(0,(X_test.shape[0])-1))
sample_index = random.sample(index, 10000)
# 模型
pred_KMedoids = KMedoids(n_clusters=12, random_state=0).fit(X_test[sample_index,:])
# 印出分群結果
pred_labels = pred_KMedoids.labels_
# 衡量結果
print(metrics.classification_report(pred_labels, Y_test.iloc[sample_index]))